Chapter 10

Put write strategy: Yield generation

In an earlier chapter, we introduced put options and used insurance as an analogy. We discussed an example where you had recently purchased a health insurance policy. You had done so that you were covered for any unplanned expenses that could arise from a medical emergency.  

Put options are similar to insurance because if you own a particular stock, you can purchase a put option on that stock to protect you from downward movements in the stock, should they occur. Since buying puts is like buying insurance, then selling puts is like selling insurance.

Warren Buffett is arguably one of the most notable and greatest investors of the last century. He is known for the conglomerate that he runs, Berkshire Hathaway, as well as notable investments in Coca-Cola, NetJets, and railroads. He is also well known for not investing during the tech boom of the late 1990s. What he isn’t well known for is GEICO - the Government Employees Insurance Company. In the US, GEICO is a property & casualty insurance company that is known for its extremely low premiums. GEICO keeps their profit margins low in order to keep their customers’ premiums low. By keeping premiums low, they can have a larger customer base with which to collect premiums from. These premiums are then invested in the markets and the company is able to earn an attractive return. 

Warren Buffett, through Berkshire Hathaway, owns GEICO and by being in the business of selling insurance, Buffett is essentially selling puts; albeit in a very sophisticated way.

Image: Warren Buffett at a GEICO corporate meeting

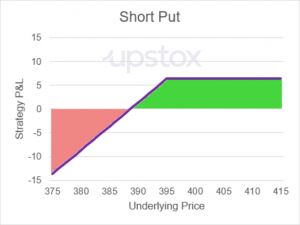
What is the maximum profit? 

The maximum profit is the premium received by selling the put option. The trader will retain this full value if the price of the underlying is above the strike price of the sold put option at expiration. 

Selling a put option is inherently a bullish strategy because if the underlying moves upward, the trader will retain the premium of the sold put option. The formula for the profit of a short (or written) put option is:

Key Formulae

Short Put Option Profit = Premium Received – Max(0, Strike Price – Underlying Price)

This formula is more complex than the previously discussed profit formulas. 

• First, the core component is the ‘Premium Received’. 
• Next, if the underlying price is above the strike price, this means that the underlying has moved upwards in a favourable direction for the trader. 
• For example, if the strike is 100 and the underlying is 120, then the second part of this formula is: ‘Max(0, 100-120)’ 
• This results in a value of zero so the profit is the premium received. 
• However, if the strike is 200 and the underlying is 150, then the second part of this formula is: ‘Max(0, 200-150)’ 

This results in a value of 50. If the premium received is more than 50, then the trade is still profitable. If the premium received is less than 50, then this trade is a loss.

What is the maximum loss? 

The maximum loss would occur if the price of the underlying goes to zero. In this rare occurrence, the loss would be the amount of the strike price offset by the premium received.

What is the break-even point? 

The break-even is a slightly different concept for writing or selling options compared to buying options. When you buy options, you have an outlay of cash that leaves you in the negative. Once the underlying moves favourably to the break-even price, your trade is now ‘in the green’ and is profitable on paper. 

When you sell an option, you receive the premium as a credit. This credit is the most profit you can make from this trade. If the price of the underlying moves towards the break-even point, this reduces your profit. Once the break-even point is crossed, you are now losing money on the trade. 

For sold (written) put options, the break-even point is the strike price of the put option minus the premium received. If the underlying stays at or above the strike price, you will retain all of your premium collected and thus earn the maximum profit.

Key Formulae

Short Put Option Break-even Point = Short Put Strike – Premium Received

Illustration 1

Put Write Example using Historical Data

Let’s assume the Nifty is trading at 16,719.45 and we are looking at options contracts that have two weeks to expiry. The 16,700-strike is the at-the-money strike price. The table below is of put options and lists the at-the-money strike as well as three additional lower strikes that are out-of-the-money.

If you were to sell a put option at the 16,500-strike, you will receive a premium of 109.60. This is more premium than you would receive should you decide to sell the 16,100-strike price as this option would only result in 36.00 in premium. For reference, this is real historical Nifty options data. 

When you sell puts, your return is known as ‘yield-to-strike’ or YTS. Yield-to-strike is calculated by dividing the premium by the strike. The YTS for the 16,500-strike is 0.66% and the YTS for the 16,100-strike is 0.22%. While this seems extremely small, the yield-to-strike is often annualised because a put option with 2 days until expiration will nearly always have a smaller yield than a put option with 2 weeks until expiration.

Illustration 2

We can annualize these returns by using the following formula:

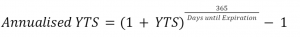
This results in an annualised yield of 18.8% for the 16,500-strike and 6.0% for the 16,100-strike. Before we make the decision that the 16,500-strike is superior to the 16,100-strike in this example, we should understand the trade-offs associated with break-even.

To the right of the bid price, we have added the break-even calculation. The break-even for the 16,500-strike is 16,390.40 which is 16,500 minus the premium received of 109.60. By comparison, the break-even for the 16,100 strike is 16,064 or 16,100 minus the premium of 36.

If you traded the 16,500-strike, then the Nifty would have to drop 1.3% in order for your trade to turn negative. Conversely, the Nifty would have to fall 3.7% in order for the 16,100-strike trade to turn negative. 

In the table above, we have also added the probability of success based on the break-even price in the column on the right. We will not discuss the calculation of this metric in this chapter but this concept is discussed in the chapter on Delta (Option Greeks). 

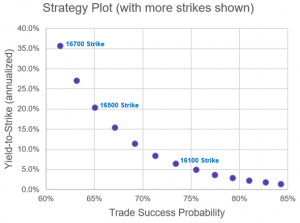
As you can see, there is a 65% chance you will not make a loss on the 16,500-strike and a 73% chance of not making losses with the 16,100-strike. Another way to think about this is: how likely is it for the Nifty to fall either 1.3% or 3.7% in two weeks? Ultimately, it is a trade-off between higher yield and lower likelihood of trade success or lower yield but higher likelihood of trade success.

In the chart below, we’ve plotted the trade success likelihood versus the yield-to-strike annualised data from this example. Remember, there is no right or wrong answer on which strike to select; it is up to the trader to determine their own risk versus reward profile.

Illustration 3

To conclude, 

• Think of Put options like insurance. They protect you from downward movements in the stock.
• Maximum profit is the premium received by selling the put option.
• The trader will profit if the underlying moves upward.
• Maximum loss occurs if the price of the underlying goes to zero.
• When selling options, the profit reduces as the price of the underlying moves towards the break-even point.
• Trader makes a loss when the price of the underlying crosses the break-even point. 
• The trader profits when underlying stays at or above the strike price and they are able to retain all their premium.
• When you sell puts, your return is known as ‘yield-to-strike’ or YTS.
• The yield-to-strike is often annualised.

Key Formulae

• Short Put Option Profit = Premium Received – Max(0, Strike Price – Underlying Price)
• Short Put Option Break-even Point = Short Put Strike – Premium Received
• Yield to strike = Premium/ Strike
• 

This concludes our module on Options Strategies. In the next module, we will see how to use options strategies in combination with equity trades. See you there.