Chapter 7

Long Strangle Option Strategy

Talk about having your cake and eating it too! In the last chapter we discussed an options strategy that helps you prepare for volatility. Now what if we were to tell you that there are not just one, but two such strategies you could choose from. ‘Two’ (pun intended) good to be true? You bet! 

Why would you use this? 

A trader will enter into a strangle if they believe that the underlying will be volatile during the period before expiry. The trade works best when the underlying is less volatile before entering the trade and then becomes more volatile during the life of the options. The trader doesn’t have a specific forecast of bullish or bearish but will be successful if movement in the security occurs.

How do you construct it? 

A long strangle is very similar to a long straddle. Both strategies are for when a trader believes that the underlying will be volatile. The difference is that a long strangle on a particular security will have a lower cost to purchase than a long straddle. However, the underlying will need to move more in order for a strangle to be profitable than for the straddle. 

A long strangle consists of purchasing both a call and a put with the same expiration date but with different strike prices. The purchased call option will have a higher strike price than the purchased put option. 

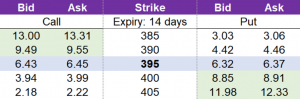
In the table below, the underlying is trading at 395 and if a trader believes that this security will move significantly from 395 in the near future, then they could enter into a strangle. 

You could select any strike but as an example, you could purchase a call on the 400-strike which would cost you the asking price of 3.99. You could also purchase a corresponding put on the 390-strike which would cost you the asking price of 4.46. Entering into the 390-400 strangle, would cost 8.45. 

By comparison, to enter into a straddle with a strike of 395 – that is centred between 390 and 400 – would cost 12.82. This is because the 395 call costs 6.45 and the 395 put costs 6.37.

Illustration 1

What is the maximum gain and profit? 

The maximum gain and profit for strangles are similar to straddles and depend on the direction in which the underlying moves. 

• If the underlying security moves upwards, then the payoff will be similar to a call option. Since only the call or the put will end up in the money, if the underlying price closes up significantly at expiration, the call will be valuable but the put will be worthless. 
• Conversely, if the underlying security moves downwards, then the payoff will mimic that of a put option. 
• If the underlying price doesn’t move enough to offset the initial cost of buying both options, your trade will end in a loss. 

The formulae for the payoff and profit of the strangle option strategy are below. 

Key Formulae

• Long Strangle Payoff = Long Call Payoff + Long Put Payoff
  • Long Call Payoff = Max(0, Underlying Price – Strike Price)
• Long Put Payoff = Max(0, Strike Price  – Underlying Price)
  • Long Strangle Profit = Straddle Payoff – Straddle Cost

What is the maximum loss? 

The maximum loss is capped at the price you paid to enter the strategy. Using the table above, if the trader entered into a 390-400 straddle, the trader will pay a total of 8.45 to purchase both the 400-strike call option and 390-strike put option. 

What is the break-even point? 

Like a long straddle, a long strangle has two break-even points. The first break-even point is the lower (put option) strike price minus the cost to enter the strategy. The second break-even point is the upper (call option) strike price plus the cost to enter the strategy. 

Key Formulae

• Long Strangle Break-even Point #1 = Strike Price – Cost of Strategy
• Long Strangle Break-even Point #2 = Strike Price + Cost of Strategy

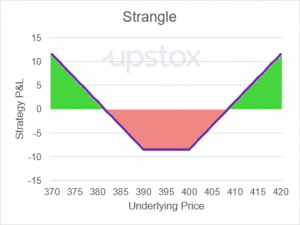
In illustration 2 below, you can see two sections that are shaded green: one to the left of the 390-strike price and one to the right of the 400-strike price. Since the total cost is 8.45 to enter this example strangle, the two break-even points would be 

1. 381.55 (390 – 8.45) 
2. and 408.45 (400 + 8.45).

Illustration 2

Strangle Scenarios using Historical Data

Let’s discuss a few examples using real market data to understand the opportunities and risks associated with straddles.

Scenario 1 – Underlying is above the upper break-even price at expiration

The Situation:

• The trader believes the Nifty will become more volatile in the next two weeks. Currently, the Nifty is trading at 17,625.70.
• The trader purchases a strangle with strike prices of 17,950 and 17,350 with expiration dates that are two weeks in the future.
• The long call option costs 57.05 for the 17,950-strike price.
• The long put option costs 77.20 for the 17,350-strike price.
• The total cost of the strangle is 134.25.
• The two break-even prices are 18,084.25 (strike price + strangle cost of 134.25) and 17,215.75 (strike price – straddle cost of 134.25).
• In order to break-even, the Nifty either needs to move up 2.6% or down 2.3%.

What happens:

• Over the course of two weeks, the Nifty trades upward and closes at 18,257.80 on expiration.
• The underlying price is above the upper break-even price so the trade is profitable.

Trade Results:

• The call option is in-the-money and has an intrinsic value of 307.80 on expiration.
• This is calculated by taking the Nifty price of 18,257.80 and subtracting the strike price of 17,950.
• The put option is out-of-the-money and has no intrinsic value because the Nifty price is above the put’s strike price.
• The net profit of the strangle is 173.55.
• This is the call option’s payoff of 307.80 subtracted from after the cost to purchase the strangle which was 134.10.
• The return on this trade is 129.3%.

Results compared to Long Straddle:

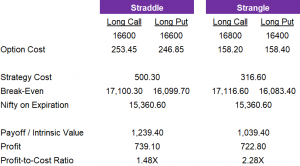
• In the table below, we compare the strangle example discussed with a comparable straddle that has a strike price at the midpoint between the strangle’s strike prices.
• The straddle is on the left while the strangle is on the right.
• To enter into the straddle, the trader would need to spend 351.10. By comparison, it would only cost 134.25 to enter the strangle.
  • However, the break-even points for the strangle are wider. The Nifty needs to move more than +2.6% or -2.3% for the strangle to break-even.
  • For the straddle, the Nifty needs to move more than +2.1% or -1.9% to break-even.
• In this particular situation, the straddle had a payoff nearly double that of the strangle: 607.80 vs. 307.80.
• Even though the cost of the straddle was higher than the strangle, the profit was still 48% higher for the straddle than the strangle: 256.70 vs. 173.55.
• While the straddle profit is higher than the strangle profit, the cost to enter the straddle was also 162% higher than the strangle (351.10 vs. 134.25).
  

Illustration 3

Scenario 2 – Underlying is below the lower break-even price at expiration

The Situation:

• The trader believes the Nifty will become more volatile in the next two weeks. Currently, the Nifty is trading at 16,628.00.
• The trader purchases a strangle with two weeks to expiry. They do this by purchasing a call option with a strike price of 16,800 and a put option with a strike price of 16,400.
• The long call option costs 158.20 and the long put option costs 158.40.
• The total cost of the straddle is 316.60.
  • The two break-even prices are 17,116.60 (strike price + strangle cost of 316.60) and 16,083.40 (strike price – strangle cost of 316.60).
• In order to break-even, the Nifty either needs to move up 2.9% or down 3.3%.

What happens:

• Over the course of two weeks, the Nifty trades downward and closes at 15,360.60 on expiration.
• The underlying price is below the lower break-even price so the trade is profitable.

Trade Results:

• The call option is out-of-the-money and has no intrinsic value because the Nifty price is below the call’s strike price.
• The put option is in-the-money with an intrinsic value of 1039.40.
• The intrinsic value is calculated by subtracting the Nifty price of 15,360.60 from the put option’s strike price of 16,400.
  • The cost to purchase the strangle was 316.60. Since the intrinsic value on expiration for the put option is 1039.40, then the net profit of the trade is 722.80 after accounting for the cost to purchase the strangle.
• The return on this trade is 228.3%.

Results compared to Long Straddle:

• In the table below, we compare the strangle example discussed with a comparable straddle that has a strike price at the midpoint between the strangle’s strike prices.
• The straddle is on the left while the strangle is on the right.
• To enter into the straddle, the trader would need to spend 500.30. By comparison, it would only cost 316.60 to enter the strangle. However, the break-even points for the strangle are slightly wider.
• In this particular situation, the straddle had a payoff that was almost 20% more than that of the strangle: 1239.40 vs. 1039.40.
• Since the cost of the straddle was higher than the strangle, the profit of the straddle wasn’t that much higher than the strangle: 739.10 vs. 722.80. 
• While the straddle’s profit was numerically higher in this example, the profit-to-cost ratio is significantly higher for the strangle.

Illustration 4

Scenario 3 – Underlying is between the two break-even points

The Situation: 

• The trader believes the Nifty, which is currently trading at 17,576.85, will be more volatile in the near future.
• The trader decides to enter into a strangle with strike prices of 17,700 and 17,500.
• The trader purchases a call option at a cost of 193.30 for the 17,700-strike price.
• They also purchase a put option for the 17,500-strike price for a cost of 207.60.
  • The total cost to enter the straddle is 400.90.
• The two break-even points are 18,100.90 (strike price + 400.90) and 17,099.10 (strike price – 400.90).
• For the strangle to become profitable, the Nifty needs to move upwards by more than 3.0% or downwards by more than 2.7%.

What happens:

• Over the course of two weeks, the Nifty trades flat and closes at 17,605.85 on expiration.
• The underlying price is between the two break-even points so the trade ends as unprofitable.

The Trade Results:

• The payoff for a call option is Max(0, Underlying – Strike).
  • Since the underlying (17,605.35) is less than the call option strike price (17,700), this means the payoff formula results in a value of 0 for this call option.

• The payoff for a put option is Max(0, Strike – Underlying).
  • Since the underlying (17,605.35) is above the strike price of the put option (17,400), the payoff of this put option is 0.

• The trader would lose 100% of their 400.90 that they paid to enter the strangle.

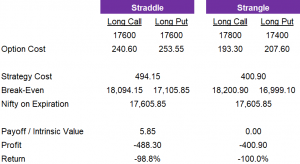
Results compared to Long Straddle:

• In the table below, we compare the strangle example discussed with a comparable straddle that has a strike price at the midpoint between the strangle’s strike prices.
• The straddle is on the left while the strangle is on the right.
• To enter into the straddle, the trader would need to spend 494.15. To enter the strangle, it would cost 400.90.
• In this particular situation, the Nifty closed slightly above the long call of the straddle. This placed the straddle’s long call ‘in-the-money’ but not enough to be profitable. The straddle ended up losing 98.8% of its value on expiration. 
• The Nifty’s closing price was lower than the strike of the strangle’s long call resulting in this option being ‘out-of-the-money.’ Also, the strangle’s long put is ‘out-of-the-money’ so both options have no intrinsic value. This leads to the strangle being a 100% loss on expiration.

Illustration 5

To Conclude:

• Use a long option strangle strategy if you believe the underlying will be volatile before expiry.
• This works best if volatility increases during the life of the options.
• Trader does not have a bullish or bearish outlook, benefits if any movement occurs in the security.
• On the same security, a long strangle will have a lower cost to purchase than a long straddle.
• The underlying will need to move more in order for a strangle to be profitable than for the straddle.
• To construct a long strangle, purchase both call and put options with the same expiry, but different strike prices.
• Buy a call option at a higher strike price than the put option.
• Maximum gain and profit depend on the direction in which the underlying moves.
• If the underlying security moves up, then the payoff will be similar to a call option.
• If the underlying security moves down, then the payoff will be similar to a put option.
• If the underlying price doesn’t move enough to offset the cost of buying both options, you will incur a loss.
• Maximum loss is capped at the price you paid to enter the strategy.
• A long strangle has two break-even points.

Key Formulae

• Long Strangle Payoff = Long Call Payoff + Long Put Payoff
  • Long Call Payoff = Max(0, Underlying Price – Strike Price)
  • Long Put Payoff = Max(0, Strike Price  – Underlying Price)
• Long Strangle Profit = Straddle Payoff – Straddle Cost
• Long Strangle Break-even Point #1 = Strike Price – Cost of Strategy
• Long Strangle Break-even Point #2 = Strike Price + Cost of Strategy

This concludes the list of options strategies you can adopt if you believe the underlying will be volatile. In the next chapter, we will focus on a strategy that you can adopt in the opposite scenario - when you think the underlying will not be volatile. See you there.