Chapter 4

Historical Volatility and Implied Volatility

Part I – Introduction to Standard Deviation

Before we explore more formal definitions of volatility, we will start with a practical example.

Let’s assume that you notice that, on average, your daily commute to work takes approximately 30 minutes. You notice though, that sometimes, it takes you more time to travel and on other days, you can arrive quicker. There is nothing really changing the traffic patterns like a major holiday – it is merely variability due to other commuters. On certain days, you have early meetings and you know that randomly, the commute could take longer than 30 minutes. You would like to know how much earlier you need to leave for work to account for the variability that occurs in your commute. To do this, you could look to a concept known as ‘standard deviation’.

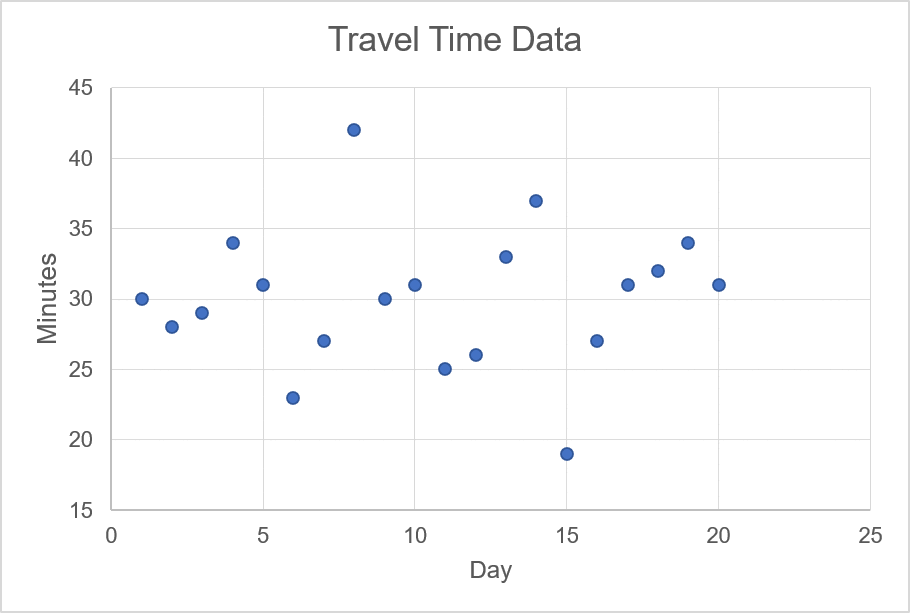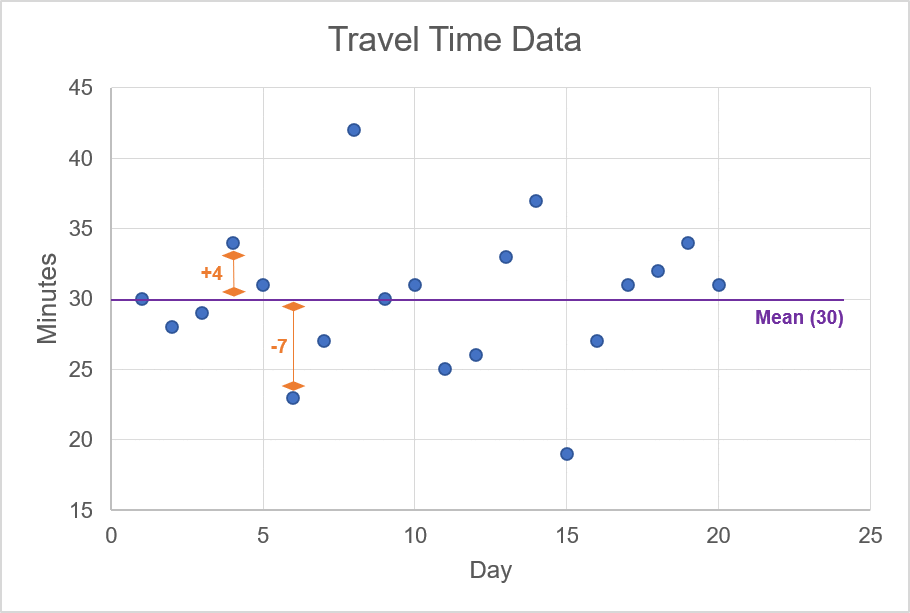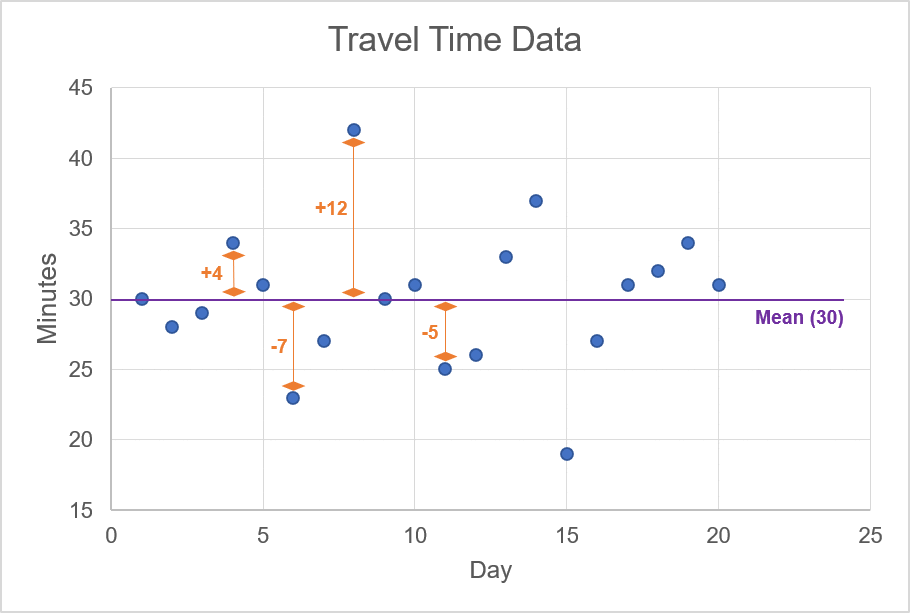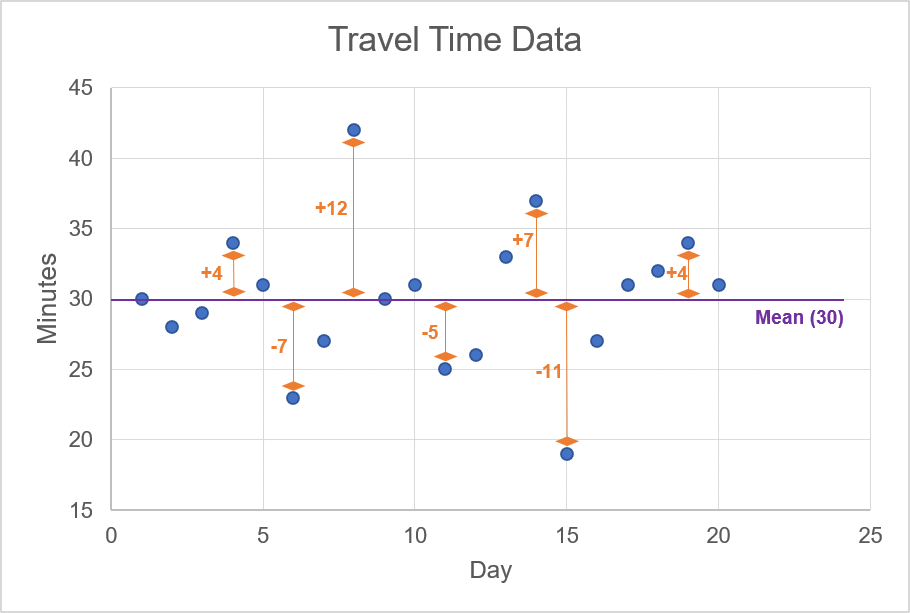
You decide to collect data over a period of 20 days to get a good estimate. The table below shows this example data.

Illustration 1

The first step is to calculate the average or the mean of the data. You had previously estimated that it took around 30 minutes each day. The way to calculate the average is to add all the observations together and then divide by the number of observations. The formula below shows this as we add all of the travel times together in the numerator. In the denominator, we have the number of observations or in this case, 20 days. 

The mean travel time is, in fact, exactly 30 minutes. 

The next step is to determine what is known as the ‘standard deviation’ or the average distance from the mean. In the chart below, we plot all of our travel observations. The y-axis on the chart is the number of minutes taken to get to the office. 

In the animation, we highlight the mean value of 30 minutes; this line cuts through the approximate centre of the scattered data points. For each one of these data points, we want to calculate the difference between the observation and the mean. For example, if the observation is 34, then the difference for this data point is +4 since the mean is 30. The animation below shows a few examples of calculating the difference between an observation of travel time and the mean of the travel times.

Illustration 2

Once you calculate the difference between each observation and the mean, you need to then: 

• Square the difference of the values
• Then add those values together 

In the table below, we carry forward the data from Illustration 1 and then perform the difference and squaring calculations.

Illustration 3

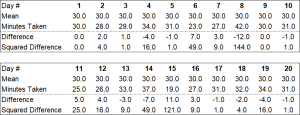
If you add all of the values in the ‘squared difference’ rows, you will get 476.0. 

The next step is to divide this by total by the number of observations minus 1. The number of observations was 20 so we would divide 476 by 19. This results in a value of 25.05. 

The last step is to take the square root of this number. The square root of 25.05 is 5.005. This is the standard deviation.

To recap, you calculate standard deviation by:

1. Subtracting the average value from each of the observations.
2. Squaring each value (the difference) from step #1.
3. Adding up all the values from step #2.
4. Subtract 1 from the number of observations.
5. Divide the result from step #3 by the result from step #4.
6. Calculate the square root of the result from step #5.

So how do you interpret this? In our example, you calculated that the average time to commute to work is 30 minutes. The standard deviation, or the average dispersion from the mean, is 5. We saw commute times that were both above and below the mean so it only makes sense that we can ‘quote’ the standard deviation in relation to the average. If we want to provide a more accurate representation of what our commute time is, we can say that it takes 30 +/- 5 minutes to commute to work. 

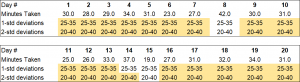
Here, The ‘5’ is one standard deviation from the mean of 30. Two standard deviations from the mean would be ‘10’ in our example. Three standard deviations would be ‘15’ and so forth. Returning to our data table, we’ve added rows that show the ranges of 1- and 2-standard deviations surrounding the mean value of 30. We are highlighting where the ranges of the 1- and 2-standard deviations include the observation. 

For example, on day 3, the observation of ‘29’ is found both within the 1-standard deviation range of 25-35 and 2-standard deviation range of 20-40. However, on day 14, the observation is not found in the 1-standard deviation range but is within the 2-standard deviation range. Observations on day 8 and day 15 aren’t found in either the 1- or 2-standard deviation range. As you can see, the 2-standard deviation includes more of the observations than the 1-standard deviation range. 

Illustration 4

Taking a step back to standard deviations, in general, 

• A 1-standard deviation plus or minus from a mean value will include approximately 68% of observations of a sample 
• On average, 2-standard deviations will include approximately 95% of observations 
• 3-standard deviations will approximately include 99.9% of observations. 

Part II – Introduction to Historical & Implied Volatility

When index or stock returns are discussed, sometimes the term ‘volatility’ arises. 

There are two types of volatility: historical volatility and implied volatility. Sometimes, historical volatility is referred to as realised volatility and implied volatility is referred to as expected volatility. 

Historical Volatility

Much like in our commute example, we would want to calculate the historical volatility of an index or scrip to see how much it has moved in the past. 

Why consider historical volatility?

Understanding the historical volatility of an index or scrip allows us to understand the potential for downward or upward price movements. With this information, we can better manage risk if we own the scrip or get a better idea as to the potential for profitability of a particular option-strike-expiration combination. 

If a scrip has low historical volatility - while it isn’t a prediction of future volatility - we can generally assume that downside risk isn’t as much as for a scrip that has had high historical volatility. 

Similarly, if we are considering buying an option and the index has had low recent historical volatility, we may use this information to make an assumption on future volatility. This could allow us to gauge the likelihood of the option ending in-the-money on expiration.

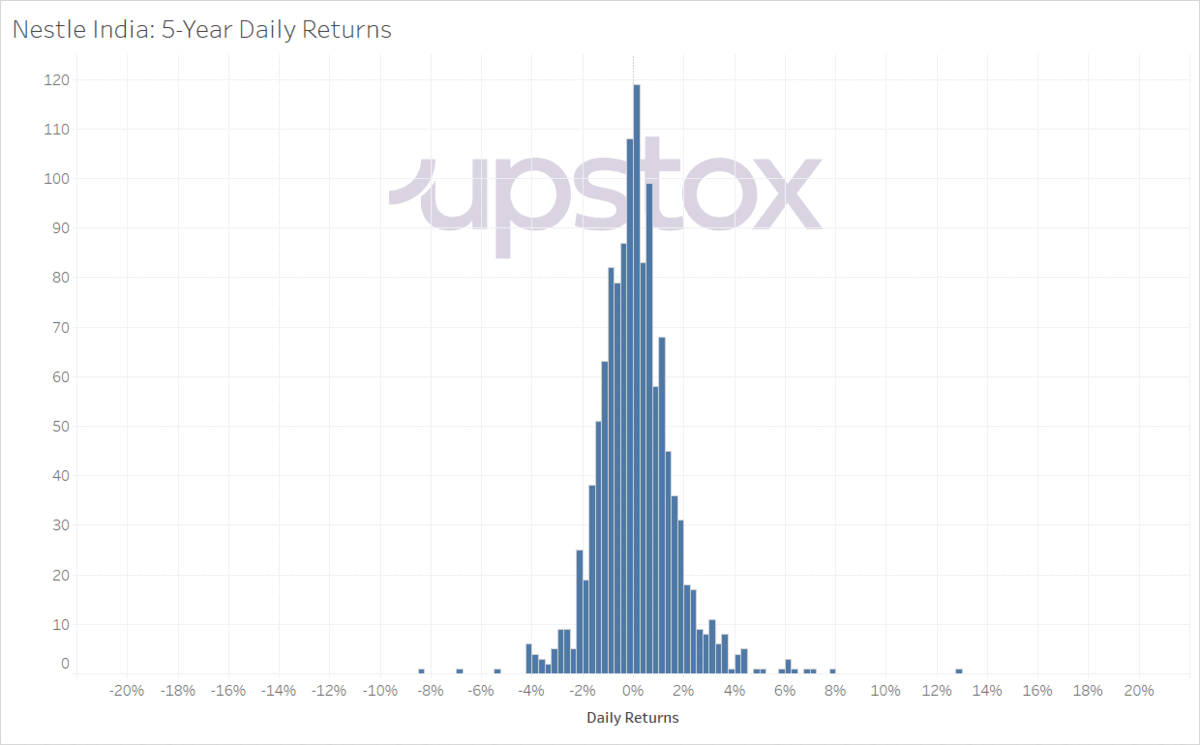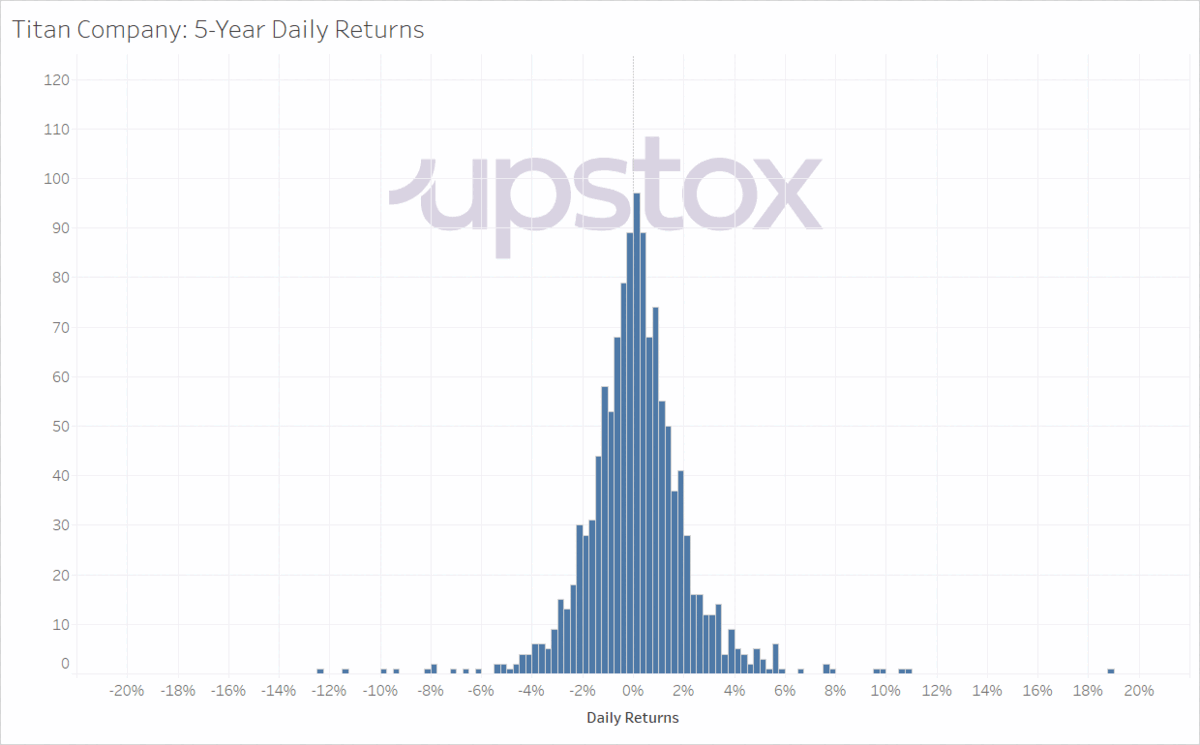
The standard deviation is a measure of spread surrounding the mean. Here are two charts that plot the daily returns for Nestle India and Titan Company for the last five years. As you can see as the charts alternate, Nestle has a lower spread surrounding the mean than Titan. 

Illustration 5: Comparison of 5-year returns of two companies

So far, we only discussed the manual way to calculate standard deviation (or historical volatility). The good news is that we don’t need to manually calculate the standard deviation as well as the mean – we can use Excel. 

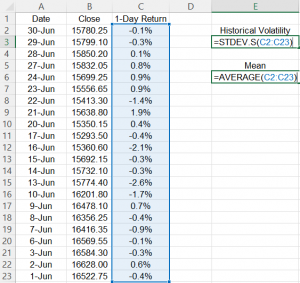
In the illustration below, we are listing the 1-Day Nifty returns for the month of June in column C. In column E, we show the Excel formula that you can use to calculate the standard deviation. Below this formula, we also provide the Excel formula for the mean.

Illustration 6: Calculating mean and standard deviation in Excel

Good to Know:

When you calculate the standard deviation for historical index and stock returns, that standard deviation is associated with the time period of the measurement. In illustration 6, we have recorded daily returns. When we use the Excel formulas to calculate the mean and historical volatility, we get -0.2% for the mean and 1.07% for the historical volatility (standard deviation). The mean value of -0.2% here is the average ‘1-Day return’; this is because we are calculating using daily returns. 

The same is true for the standard deviation. If we want to understand the standard deviation over a different time period, we need to convert it. For example, if we want to understand the annualised historical volatility, or how much the index varied around the mean returns over the last year, we would convert this using the following factor: multiply by the square root of 252.

So, for the annualised volatility calculated based on daily historical returns, we would multiply 1.07% by √252. We do this by ‘252’ because this is the approximate number of trading days in a year. 

If we have an annual historical volatility number and we wanted to understand the weekly volatility, we would divide by √52. We use ‘52’ because that is the number of trading weeks in the year. For example, if we know that a stock has a historical annual volatility of 20% and we want to know how much the stock could move within a week, on average, the historical weekly volatility is 2.8% (or 20% divided by / √52).

As a trader, you can look at historical returns data and calculate the historical volatility. 

Understanding Implied Volatility

For implied volatility, you don’t need to calculate anything; you only need to look to the Option Chain. We will be covering the option chain in the next chapter. For now, all you need to know is that there will be an implied volatility value associated with each call and put option. 

The implied volatility is the market’s expectation of future volatility. It is based on the supply-demand relationship for the option. If there are more buyers of an option than sellers, the option price will go up as well as the implied volatility. Conversely, if there are more sellers than buyers of an option, the option price will go down along with the implied volatility. 

The implied volatility for options as seen in an options chain is the annualised volatility – if you want to use this to estimate different timeframes, you would need to convert as discussed in the previous paragraph. Another way to think about implied volatility is that it shows how uncertain the market is about a particular security. 

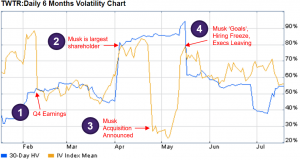
Illustration 7 below shows the historical and implied volatility of Twitter. The blue line is the trailing 30-day historical volatility. The yellow line is the average implied volatility across all of the options for Twitter that expire in 30-days. This chart shows this for approximately the first half of 2022. 

As you can see, implied volatility does not always equal historical volatility. In this chart, one line is looking 30-days back while the other is what the market is ‘thinking’ about in terms of 30-days into the future. There are four points that are illustrative of this ‘thinking’.

1. The first highlighted point is near the first week of February. The implied volatility climbs throughout the end of January and on a single day, drops from almost 90% to 50%. This was due to the Q4 earnings. Implied volatility rose as there was uncertainty as to the contents of the earnings release. Once that information was released, then the uncertainty of the information reduced dramatically. For reference, this is a common phenomenon associated with implied volatility around earnings announcements.
2. At the second highlighted point, there is a spike in volatility from 45% to 80%. This movement in implied volatility happens within 1-2 weeks. This occurs when there was information leaked and then eventually confirmed, that Elon Musk had acquired a substantial amount of Twitter stock. Implied volatility went up because there was uncertainty as to what Musk’s intent with Twitter was.
   
3. At the third highlighted point, you can see a reduction in implied volatility from 80% to 30%. This is when it was announced that Musk was planning to acquire Twitter. This reduced the uncertainty due to his acquisition of Twitter shares.
   
4. Lastly, the fourth highlighted point shows an increase from 25% to 80% implied volatility. This occurred following the release of Musk’s goals for the company, an announcement of a hiring freeze, and news that several executives were departing. This information created uncertainty in the market in terms of Musk’s management of Twitter, its financial strength, and its ability to attract and retain talent.
   

Illustration 7: Twitter Historical Implied and Historical Volatility

To Conclude:

• There are two types of volatility: historical volatility and implied volatility.
• Historical volatility is also called realised volatility. 
• Historical volatility helps estimate potential for downward or upward price movements of an index or scrip. 
• One can assume that a scrip with low historical volatility has a lower downside risk compared to one with high historical volatility.
• Use Historical volatility to estimate the profit potential for a particular option-strike-expiration combination.
• Implied volatility is also called expected volatility.
• Implied volatility is the market’s expectation of future volatility.
• More the buyers for an option, the higher the option price and its implied volatility.
• More the sellers for an option, the lower the option price and its implied volatility.
• Study the Option Chain to understand implied volatility of an option. The Options chain gives the annualised volatility of an option.

In summary, historical volatility is a backward-looking, realised view of volatility and can be calculated using the standard deviation formula. 

While implied volatility can’t be calculated using the standard deviation formula, it is the market’s expectation for upcoming standard deviation. 

If the implied volatility for options that expire in 30-days is 15%, this means that the market is expecting the standard deviation for the underlying to be 15% on an annualised basis. Since the option expires in 1-month, we can calculate how much the market is expecting the underlying to move in that 1-month period. Dividing the 15% by the square root of 12 results in 4.3%. Therefore, at the one-standard deviation level, the market is expecting 68% of observations of the underlying’s return to be within +/- 4.3%.