Chapter 1

Volatility

To introduce the concept of time value and intrinsic value, let’s go back to the long days of summer. What is the best part about summer, apart from school vacations? You bet! Those ripe, juicy, golden mangoes that we can’t get enough of. 

How is that related to Time Value and Intrinsic Value? Let us show you.

Now, unless you have access to a mango tree, the mangoes you eat come in baskets or crates wrapped in newspaper and straw. Most of these would be unripe or nearing ripeness. This critical point is when the farmer gets the best price for the mangoes. 

But, the price of the mango is also dependent on which variant it is. The most expensive are the Alphonso mangoes or the Hapus which are prized for their sweetness. The Time Value and Intrinsic Value of an options contract is somewhat similar. 

As the time to expiry increases, the price of an options contract also increases. Just like the mangoes being priciest when they are at the near-ripe stage. However, the price of an options contract is also dependent on the value of the underlying. Just like you would pay more for the Hapus as compared to a Totapuri.

Now that the concept of time value and intrinsic value is clear, let’s understand this better with a previously used example.

In this example, it was 16 June 2022 and you were bullish on the Nifty 50 over the next two weeks. The current price of the Nifty then was 15,360.60 and you decided to purchase a call option with a strike price of 15,350. You selected this strike price because it was the closest to where the Nifty was trading at. The market price for this call option on the Nifty 50 with a strike price of 15,350 that expired on 30 June 2022 was ₹285.35. 

What is Intrinsic Value?

As we’ve learned previously, if the price of the underlying stock or index is higher than a call option’s strike price, then the call option is in-the-money and has intrinsic value. In this case, the intrinsic value was ₹10.60. 

Below, we calculate the intrinsic value for this call option.  

Nifty’s price - the strike price = Intrinsic value 

i.e. 15,360.60 - 15,350 = 10.60 

Here is a diagram using this example to help understand the relationship between strike price, underlying price, intrinsic value, and break-even for call options.

Illustration 1

So, if the intrinsic value of this call option is only ₹10.60, then why are we paying ₹285.35 for this option? The answer is time value. 

What is Time Value?

There is a saying that ‘time is money’ and it certainly applies to option prices. Here is why: 

• The more time between now and the expiration of the option, then there is more of a chance that the underlying can move 
• The more that the underlying can move, then there is a higher chance that the option could have intrinsic value 

Let’s review historical data to be more objective with this concept.

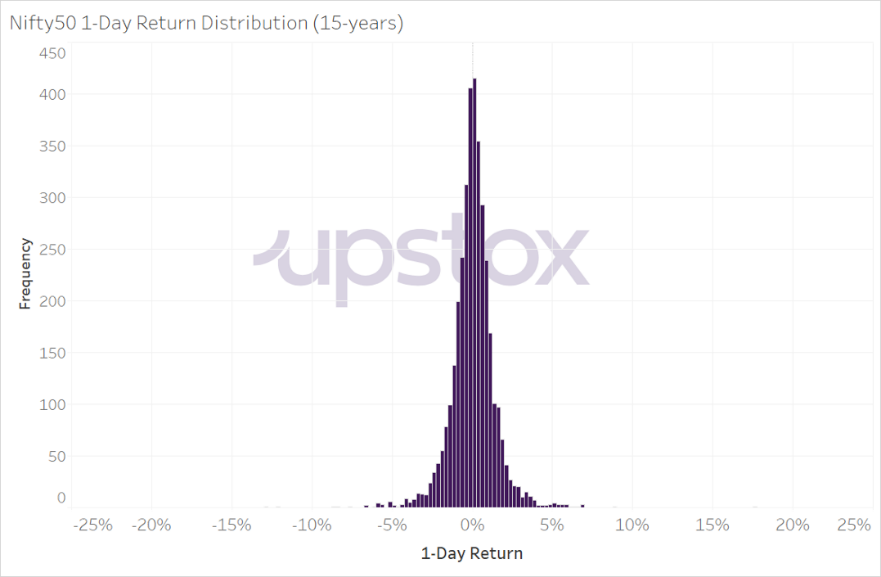
Below is a histogram that charts the distribution of the Nifty50 1-day returns over the last 15 years. On the horizontal axis are 1-day return ‘bins’. The vertical axis is the frequency of observations associated with those bins. If there is only one observation (or day) where the Nifty returned +10%, then the frequency of the vertical axis would be 1 for the +10% value on the horizontal axis. 

As you can see, there are a large number of observations centred around 0% with few observations outside that are greater than +5% or less than -5%. On an average over the last 15 years, the daily return of the Nifty50 was 0.04%. The standard deviation is 1.40%. (We will cover more details on standard deviation in our chapter on volatility. For now, all we need to know is that it helps give us a range of values). If you add the standard deviation to the average as well as subtract the standard deviation from the average, you will have a range that contains approximately 68% of values. 

Based on this information, we can say that 68% of 1-day returns of the Nifty50 index over the last 15 years were between +1.44% and -1.36%.

Illustration 2: 1-Day Returns of Nifty 50 for last 15 years

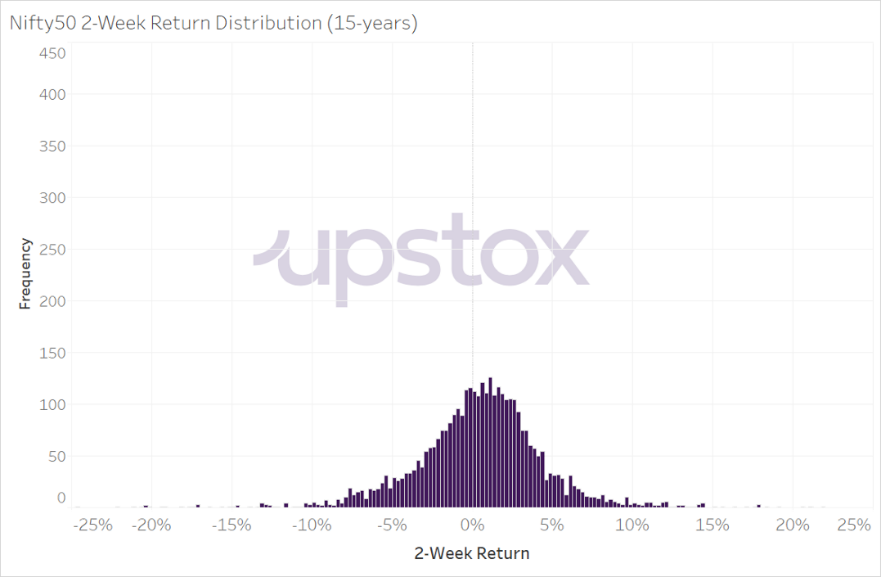
A comparison to the 1-day returns is seen in the chart below. This histogram chart plots the 2-week returns of the Nifty50 over the last 15 years. Visually, you can see that the distribution is ‘flatter’ and there are more observations that extend out to beyond +10% and -10%. On an average, the 2-week return of the Nifty50 was 0.42% with a standard deviation of 4.25%. Performing a similar analysis as above, the range of values that represents approximately 68% of observations is 4.67% and -3.83%. 

On the upper end for the 2-week returns is +4.67% which is substantively more than the upper end of the 1-day return range of +1.44%. The same is true when you compare the lower end of the 2-week returns of -3.83% to the lower end of the 1-day return of -1.36%.

Illustration 3: 2-Week Returns of Nifty 50 for last 15 years

Let’s return one more time to our call option example where we purchased a call with a strike of 15,350. This option cost us ₹285.35 making our break-even price (strike price + option price) equal to 15,635.35 (strike price + option price). 

When we bought this option, the Nifty was trading at 15,360.60. In order for us to break-even and start turning a profit, the Nifty needs to rise from the current price of 15,360.60 to 15,635.35. This is a return of 1.79%. As seen in our historical distribution data, having a return of +1.79% is far more likely to occur over a two-week period rather than a 1-day period. So, time really does equal money. Since, the intrinsic value is ₹10.60 (15,360 – 15,350), the time value is the difference in option price and intrinsic value or ₹274.75. 

Key Formulae:

Time Value = Option Price - Intrinsic Value

What this means is you are paying ₹274.75 for the two weeks of time to hold this option. If you had purchased an option with more time until expiration, assuming all other parameters like strike price were the same, you would pay more for this option due to time value. 

Just like you would pay more for a crate of mangoes nearing ripeness. Much more if they were Alphonsos!

To Conclude:

• Options pricing is a function of its Time value and Intrinsic Value.
• As the time to expiry increases, the price of an options contract also increases. This is Time Value.
• The price of an options contract is also dependent on the value of the underlying. This is its Intrinsic Value.