Chapter 3
Vega
In previous chapters, we have covered two different option Greeks so far: Delta and Theta. The Greeks tell us how much the price of the option is expected to change based on the change in something else. Delta tells us how much the price of the option will change based on the change in price of the underlying. Theta informs us how much the price of the option will change based on time passing and the option getting closer to its expiration date. The next Greek we will cover is ‘Vega’.
Here’s a simple analogy to understand Vega better. If you have ever driven a car (or even sat in one), you will get this. Floor the accelerator and the car zooms ahead. Release the pressure on the accelerator and the speeding car slows down.
The relationship between Vega, Volatility and the Option price is very similar. Any increase in implied volatility leads to an increase in the option price. Conversely, any decrease in implied volatility will result in a reduction in the option price. The quantum of increase or decrease here is Vega. Thus, Vega provides us insights into how much the price of the option will change based on the change in implied volatility.
Good To Know
If it is hard to remember what Vega tells us, look to the first letter: V for Vega and Volatility.
Vega provides us insights into how much the price of the option will change based on the change in implied volatility. If it is hard to remember what Vega tells us, look to the first letter: V for Vega and Volatility.
How Vega Works
Let's look at a quick example. On 6 September, the Nifty closed at 17,665. A trader currently owns a call option on the Nifty with a strike price of 17,650. This option expires in a little over a week on 15 September. This trader wants to understand how much the option price will move if there is a spike in implied volatility.
Currently, the option's price is 211.60 and the implied volatility is 18.42%. What if the implied volatility went up 2% to 20.42%? The vega for this strike price is 11.06. This means that for each one percent increase in implied volatility, the price of the option will increase by 11.06. For the trader, the option price will go up from 211.60 to 233.72 (+22.12) if they are correct in their forecast about the 2% increase in implied volatility.
In our example, the trader owned – or was long – a call option. Since the trader was long the option, the Vega will be ‘positive’ meaning that an increase in implied volatility will lead to an increase in option price. We know that implied volatility can go up and go down. If implied volatility goes down and the trader is long the option, the option price will go down. Using our example, if instead of going up 2%, perhaps implied volatility goes down 1%. If this happens, then the price of the option will go from 211.60 to 200.54 (-11.06).
The vega for call options and put options are the same; vega only varies by strike price and expiration date for an underlying security. In our example, the 11.06 vega for the call option with a strike price of 17,650 is the same for the put option with the same strike price.
What if a trader is short a call or a put option? Instead of the vega being a positive value, it will be a negative value. For example, if our trader was instead short the call option, the vega would be -11.06. So, if the implied volatility went up by 1% while the trader is short this call option, the price of the option will go against the trader by -11.06.
How does Vega vary by time until expiration?
The level of vega will vary by time until expiration as well as moneyness.
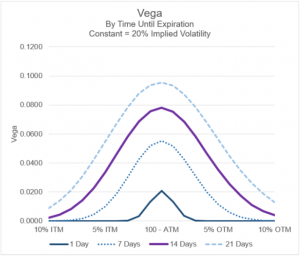
In illustration 1 below, we plot the vega for a hypothetical stock with four different times until expiration: 1 day, 7 days, 14 days, and 21 days. We are keeping implied volatility constant at 20% for each of these expiration periods. The underlying price is assumed to be 100.
On the vertical axis of the chart is the value for vega. On the horizontal axis of the chart is the moneyness of the option. The ‘at-the-money’ option is in the middle. If you go to the left, we plot the values for 1% in-the-money to 10% in-the-money. If you look to the right of the at-the-money option, we plot the values for 1% out-of-the-money to 10% out-of-the-money.
As you can see in the chart below, the values of vega by moneyness follow a bell-shaped curve. The vega values for an expiration date of 1 day are very small with the exception of an option that is close to being at-the-money. The at-the-money value for the 1 day until expiration in this example is 0.02.
By comparison, for an option with 7 days until expiration that has a moneyness of either +5% or -5%, also has a vega of approximately 0.02. Also, by comparison, an option with 14 days until expiration that is at-the-money has a vega of 0.08.
If nothing else changed except the option went from 14 days to 1 day until expiration, the vega will drop from 0.08 to 0.02. Intuitively, this makes sense because implied volatility is a forward-looking value. With lesser time between ‘right now’ and expiration, there is lesser opportunity for volatility to impact the underlying price and thus impact the option price. Vega is intrinsically reflecting this by decreasing as the option gets closer to expiry
Illustration 1
How does Vega vary by level of implied volatility?
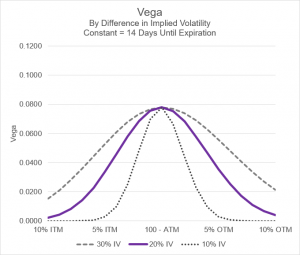
While vega tells the trader what the impact of a change in implied volatility will be, the starting level of implied volatility will impact vega. In illustration 2, we plot vega for three different levels of implied volatility: 10%, 20%, and 30%. We are looking at the expiration date that is 14 days in the future.
These charts follow a similar bell-shaped curve as seen above. As you can see, the higher the starting level of implied volatility, the higher the amount of vega. However, this doesn’t apply to the at-the-money value. Regardless of the current amount of implied volatility, the vega will be the same for the at-the-money option. When you look at the in-the-money and out-of-the-money options, you will see differing levels of vega. For example, the 5% out-of-the-money (as well as the 5% in-the-money) option will have a near zero vega when the implied volatility is 10%. For the same moneyness values but at 30% implied volatility, vega will be higher and around 0.05.
Illustration 2
As a recap, Vega helps the trader understand how the price of the option they are holding will change based on changes in implied volatility. Typically, implied volatility increases the most when the underlying stock falls. If the underlying stock falls, then the option’s price will fall. However, the increase in implied volatility will partially offset the option’s drop in value due to the decrease in the underlying price. Vega tells you how much this ‘offset’ could possibly be.
Separately, when a trader shorts an option, they could do so because they believe that the option is overpriced due to a mispricing of volatility. If the implied volatility is high and the trader believes it will revert to the historical volatility, the trader may decide to short an option. In doing so, the trader can look to the vega to see how much they could gain for each percent decrease in implied volatility.
To conclude:
- Use Vega to estimate change in option price due to implied volatility
- Vega is the same for call and put option
- Vega is positive when a trader is long a call or put option
- Vega is negative when a trader is short a call or put option
- Vega varies according to strike price and expiry
- Vega varies by time: lesser time to expiry, lesser is the vega
- Starting point of volatility also impacts Vega. Higher the starting level of implied volatility, the higher the amount of vega
That concludes our chapter on Vega. Up next is Gamma which helps estimate the rate of change in Delta.