Chapter 2

Theta

It is a dilemma we have all faced, at some point in time. You have a headache. You pull out a strip of tablets from the medicine cabinet, only to find the tablet has two days to expiry. You are now torn- have the tablet, cure the headache immediately or toss it out and buy a new one. This is because with medicines, the expiry date only tells you for how much longer the tablet is ‘safe’ to be consumed. What it doesn’t tell you is if the ‘potency’ of the medicine is still what it was when it was manufactured. 

An options trader has to similarly contend with expiry and the time decay that occurs in options contracts nearing expiration. Fortunately, unlike with medicines, there is an indicator for Options traders that takes the guesswork out of trading near expiration dates. 

Meet ‘Theta’.

This Greek is important to understand if you plan to hold an option for more than a day. 

What is Theta?

Options that are purchased lose value over time until the ‘time value’ decays to zero at expiration. At expiration, the option is either worth its intrinsic value or it is worthless depending on where the underlying price is in relation to the strike price. 

Theta provides the trader with insights into how much the option will lose in value if they continue to hold it for one more day. For example, if the price of an option right now is 1.00 and its theta is -0.05, then the option will be worth 0.95 the next day, if nothing else changes.

How to track Time Decay using Theta? 

Below, we have a combined chart that shows the loss in value of an option due to time decay. The assumption is that the underlying price or implied volatility doesn’t move; the only change is in time. We are also assuming that this option doesn’t have intrinsic value and the only value is time value. 

The top chart is a stacked bar chart that displays the change in value as the number of days until expiration. On the left side of the chart, the option has 25 days until expiration and at the far-right side of the chart, there are no days remaining until expiration. 

The purple bar shows the current price of the option. At 25 days until expiration, the option price is 2.19 and the theta is -0.04. At 24 days until expiration, the option price is 2.15 and the theta is -0.05. At 23 days until expiration the option price is 2.10. As you can see, subtracting the theta (-0.04) from the current option price (2.19) tells you what the option price will be the next day (2.15), assuming the only thing that changes is time. You can see that this follows with 24 days until expiration as you can combine the option price of 2.15 with the theta of -0.05 to get the option price of 2.10 for the next day.

Illustration 1

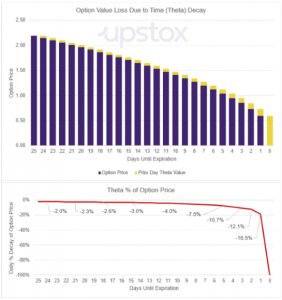
In the stacked bar chart, the yellow section of each bar is the theta value for the earlier day. So, the bar at the 2nd to the left is 24 days until expiration. The purple section plots the value of 2.15 and the small yellow section on top of that is 0.04. The total height of the purple and yellow sections at 24 days until expiration will equal the prior day’s value of 2.19. 

This chart is our way of showing not just the reduction in value of the option price (in purple) but the increasing amount of theta (in yellow).

More explicitly, the bottom chart shows the theta as a percentage of the option price. As a reminder, this option doesn’t have intrinsic value and only has time value. At 24 days until expiration, the percent of value of the option lost on that day due to theta (or time) decay is approximately 2%. Two weeks later with 10 days until expiration, you are losing 4% of the option per day due to theta decay. 

Beyond this point, the loss in value of the option due to time becomes exponential. At 7 days until expiration, you lose 7-8% by holding the option one more day due to theta decay. From 1-3 days until expiration, you are now losing up to 20% of the option’s value each day. On the last day, you lose the rest of the time value.

How Moneyness & Volatility impacts Theta?

Earlier, we looked at an example where the underlying security of an option didn’t have intrinsic value, the price didn’t change, and the volatility didn’t change. The only thing that changed was time. 

The value for theta can however, be impacted by moneyness as well as volatility. What this means is that the time decay on any given number of days until expiration could vary based on moneyness and volatility. 

In illustration 2 below, we plot theta versus moneyness for several hypothetical options with different amounts of time until expiration. 

The purple line represents the most time until expiration; the orange line is the least amount of time until expiration. The centre of the horizontal axis is the at-the-money strike. To the left is ‘in-the-money’ and to the right is ‘out-of-the-money’ on this x-axis. 

The most amount of theta decay occurs ‘at-the-money’. As you move away from being at-the-money, time decay has less impact. However, this difference in impact between moneyness is less pronounced as you have more time until expiration. When you compare the purple line with 25 days until expiration to the orange line with 5 days until expiration, the purple line is ‘flatter’ as you move from in-the-money to at-the-money and then to out-of-the-money. 

One last point is that you can clearly see the difference in theta based on time until expiration. Looking at the  centre of the x-axis, the purple line with 25 days until expiration has a theta of approximately -0.04. The orange line with 5 days until expiration has a theta of -0.09.

Illustration 2

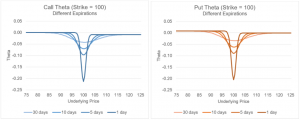
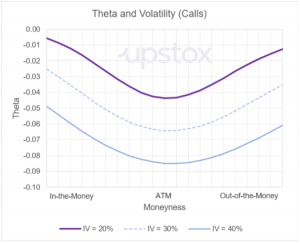
Illustration 2 plots the theta values versus option moneyness for three different levels of implied volatility. As with the previous chart, you can see the larger impact of theta associated with the at-the-money options compared to in-the-money and out-of-the-money options. 

A new call-out is that the higher the implied volatility, the larger the impact of theta. An at-the-money option in the chart below with an implied volatility of 40% has a theta of -0.085 compared to a theta of -0.042 with an implied volatility of 20%.

Illustration 3

Here are the key takeaways when it comes to Theta:

• Time decay increases closer to expiry: It is extremely difficult to fight the time decay associated with an option with limited time until expiration. If an option is losing 5%, 10%, or more in value due to time decay, the underlying will need to move even more to have a chance for the trade to be profitable.
  
• Theta is a negative value: Theta is sometimes quoted as a positive value. This is merely a simplified convention. The concept to remember is that if you buy an option, the theta is a negative value (even if quoted as a positive one).
  
• For sellers, it’s always Advantage Theta: When you are long either with a call or put option, you are exposed to theta decay. Selling calls and puts places theta as an advantage for you since your goal is for the option to expire worthless when shorting options.
  
• Fight Theta decay with Option strategies: Trading option spread strategies reduce the negative impact of theta decay. For example, if you bought an at-the-money call option, with two weeks until expiration, the theta for that day could be 0.05. If you instead bought a call spread using that same long call along with a short out-of-the-money call, the OTM call could have a theta of 0.03. 

The long call has a time decay working against you of 0.05 while the short call has a time decay of 0.03 working for you. The net theta is a negative 0.02. Instead of losing 0.05 for holding a call option for one day, you would only lose 0.02 for the day by holding a call spread strategy. You would still be impacted by theta but the amount would be reduced dramatically.

We have seen the impact of various factors on option price (Delta) and the impact of time decay (Theta). Up next, how to account for the impact of volatility in our chapter on Vega. See you there.