Chapter 1

Delta

Option Greeks are data points that provide information on the option’s price sensitivity to changes in certain parameters. There are five primary option Greeks: Delta, Gamma, Theta, Vega, and Rho. These data points help traders understand how much the option’s price could change if the underlying price changed, volatility changed, etc. 

Typically, the Greeks are found on the Option Chain and are listed along with the option’s price, strike, volume, and open interest. Unfortunately, not all financial services firms provide this critical data. We will start by exploring Delta so you can understand how this information can be valuable insight in your trading arsenal.

Why do you need Delta?

Delta is arguably the most important of the Greeks. There are three insights that Delta can tell a trader:

1. How much the price of the option will change if the price of the underlying stock or index changes
2. The ‘Hedge Ratio’
3. The approximate likelihood of moneyness on expiration

What is Delta?

The analogy of a home loan could prove useful to understand Delta. You know how it works. If the interest rate on your home loan were to increase, your EMIs (monthly instalments) would correspondingly go up. Similarly, if rates were to decrease, theoretically, your EMIs should also go down. 

Delta is similarly linked to the price of the underlying security. Delta tells you how much is the quantum of increase or decrease you can expect in option premium when the price of the underlying stock increases or decreases. In that context, look at the following example to understand how you can use Delta to understand price change, hedge ratio and moneyness on expiry. 

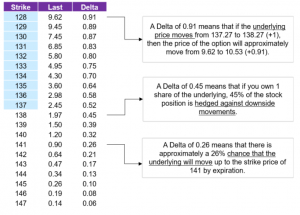
Assume that the underlying price is 137.27, and there are 4 days until expiration. (For reference, this is real historical data). 

• The table lists strike prices from 128 to 147 for a call option. 
• The strike prices that are greater than 137 are in-the-money. 
• In the middle column, is the last traded price for each of the respective strike prices. 
• The right column in the table lists the Deltas associated with the respective strike prices. 

Good to know

When you look at the table, you will see that as the strike price lowers (for call options), the delta gets bigger and appears to approach 1. When the strike price increases (for call options), the delta gets smaller and appears to approach 0. 

If we were to expand this table, you would see that the bounds of delta for call options are between 0 and 1. (While we don’t display it here, the bounds of delta for put options are between -1 and 0).

Illustration 1

Insight #1: The Delta-Price link

In the first call-out box in illustration 1 above, we highlight how delta informs us about the change in the option price. For the 128-strike price, the last traded price was 9.62 and the current delta is 0.91. This can be interpreted as if the underlying stock moves +1, then the option price will move +0.91. 

So, if the underlying price went up by 1 (or 0.73%) from 137.27 to 138.27, then the option price will move up from 9.62 to 10.53. This gain of 0.91 in the option price represents a percent gain of 9.46%. 

Good to know

When we talk about ‘Delta’, we do it in units rather than decimals. Instead of saying “delta of point nine-one” or “delta of ninety-one percent,” we simply say “ninety-one delta” or “delta of ninety-one.” 

This strike price of 128 is deep in-the-money as the underlying stock would need to drop 6.75% in the next 4 days in order for this strike to no longer be in-the-money. 

Good to know

An interesting feature: the delta gets bigger as you go deeper in-the-money, and the delta gets smaller as you go further out-of-the-money. 

In fact, the delta is close to 0.50 for the at-the-money strike. 

Thus, Delta informs you of the relationship between moneyness and how sensitive the option is to a change in the underlying price. The more in-the-money an option is, the more sensitive to the change in the underlying price. At some point, a call option will be so in-the-money that the delta will be 1 or close to 1. This means that the option essentially trades in lock-step with the underlying. As briefly mentioned before, put options have delta values that range from 0 to -1. For put options, deep in-the-money contracts have a delta of -1 or close to -1. In illustration 2 below, we plot the delta values for a call and put option across various levels of moneyness and time until expiration.

Illustration 2

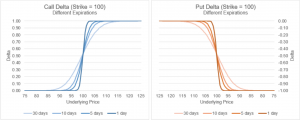
A bit of trivia: at some Wall Street firms, the equity trading desks are known as ‘Delta One’. 

In illustration 1, you can also see that the majority of the option’s price for the 128 strike derives from intrinsic value rather than time value. The intrinsic value of this strike is 9.27 (137.27 – 128). The time value for the 128 strike is only 0.35 because the option’s price is 9.62 and the intrinsic value is 9.35. 

Intuitively, this makes sense as we discussed previously that time value is derived from the volatility of the underlying stock. This is because a higher volatility could lead to an increased likelihood of being in-the-money. For a strike that is already deep in-the-money, volatility will have less impact on the likelihood of being in or out of the money at expiration.

Insight #2: The Delta & Hedge Ratio

In the middle call-out box in illustration 1, we are looking at the “‘45 delta’” line. 

The Hedge Ratio is an advanced concept that is related to delta hedging for more professional traders and market making so we will only discuss this briefly. If you were to buy the option with the 138-strike, you are now "long delta" , i.e., you have exposure to market movements. 

For most individuals reading this chapter, that is where you want to be because you are placing a trade based on your prediction for where the market will go. 

Conversely, market makers aren't concerned with making proprietary trades on market movements. They are only interested in facilitating market transactions. Instead of making a return if their predicted movement is correct, their return is based on earning the difference between the bid and the ask price. A market maker will want to hedge the delta so they have as minimal exposure to market movements as possible. 

In this example, the 45-delta would tell the market maker that they need to sell the underlying stock at a rate of 0.45 for every 1 call option purchased in order to have a delta of 0. Having a delta of 0 is considered to be “delta neutral”. Delta hedging is strictly for market makers. But this concept can be used by traders as they construct stock and option portfolios.

Good to know: How you can use Delta Hedging

If a trader wanted to reduce a particular stock’s exposure to market movements, they could use the delta to understand how many put options they should purchase to reduce this exposure. Since the trader is long on the stock, they are long on delta via an underlying. 

To reduce the delta, they would need to buy a put option rather than a call option because a put has negative delta. 

Insight #3: The Delta & Moneyness

In illustration 1, the bottom call-out box provides us with an example of a very interesting piece of information. This  is the approximate likelihood of moneyness on expiry. 

For example, the 141-strike has a delta of 0.26. This means that the market is implying that there is a 26% likelihood of the underlying being at or above 141 on expiration. This likelihood isn’t a certainty and is just a prediction based on the market’s trading of various option contracts. 

A technical point you need to know here is that there is a more accurate view of the likelihood of moneyness: this term is known as ‘Dual Delta.’ This is a more advanced topic that we won’t cover in this course. However, the difference is usually non-impactful to your decisions. In our example, the delta is 26% for the 141-strike but the dual delta could be 25%. As a trader making a quick buy or sell decision, that difference is most likely negligible. 

Let’s take this one step forward. You believe that the underlying in this example will move upwards dramatically over the next four days, so you decide to purchase the call option with a 141-strike. 

The price of this option is 0.90 making the break-even price 141.90 (141 + 0.90). 

The delta that you are most interested in looking at is the delta for the 142-strike because it is closest to the break-even price. This strike price has a delta of 0.21 meaning that the market is giving the underlying an approximate 21% chance of being at or above the break-even price.

To conclude: 

• Delta tells you how much the price of an option could change if the price of the underlying changes.
• Delta helps determine Hedge Ratio of the option to the underlying stock.
• Delta shows you approximate likelihood of moneyness on expiration.
• Delta for call options ranges from 0 to 1 and delta for put options ranges from -1 to 0.
• In a call option, as strike price reduces, delta gets bigger and vice-versa. The opposite is true for put options. 
• The delta gets bigger as you go deeper in-the-money, and smaller as you go further out-of-the-money.
• The more in-the-money an option is, the more sensitive to the change in the underlying price.
• When Delta is 1 or close to 1, the option trades in lock-step with the underlying.
• Being ‘long delta’ means being exposed to market movements – ideal for traders.
• Hedging the delta allows minimal exposure to market movements.
• Hedge delta of a stock by buying a put option for the same stock.

This concludes our chapter on the first and most important of the Greeks - The Delta. Use it to hedge your losses if you plan to trade intraday in a stock.  Up next, is an explainer on Theta. See you there.