What is call writing?
Written by Upstox Desk
Published on July 31, 2025 | 5 min read

Call writing meaning
Call writing simply refers to selling a call option contract. A call option is a type of derivative contract that derives its value from the underlying asset where the buyer benefits from an up move in the underlying and the seller (or writer) benefits from a fall or range bound movement of the underlying.
A call option buyer has the right to buy the underlying asset at a predetermined strike price, at a predetermined time. Similarly, the call option seller, also known as 'the writer', has an obligation to sell the underlying asset at the predetermined strike price when the buyer of the call option exercises this option.
Call writing example
The call option writer is obligated to sell the contract even if he is making a loss. So why does he do it?
Let's understand the call writing with the help of an example.
Mr.Kumar is an options trader. He has a range-bound outlook on Infosys, which currently trades at ₹1,800. He thinks that the price of Infosys will not move above ₹2,000 in the near term.
In order to earn profit, he decides to sell one lot of Infosys 2,000 strike price call option of the current month's expiry for the premium of ₹100.
Here,
Underlying: Infosys
Expiry: Current month
Strike price: ₹2,000
Lot size: 300
Premium received: ₹100
Total premium received: Lot size x premium received = 300 x 100 = ₹30,000.
Break even point = Strike price + premium received = 2,000 + 100 = ₹2,100.
At this point neither of them earns a profit or a loss.
Scenario 1: At expiry, Infosys is trading at ₹2,300.
In this case, his view turned out to be incorrect and the spot price moved higher than the strike price. Hence, Mr. Kumar will incur a loss. The extent of the loss, however, will be the difference between the spot price and breakeven point.
Loss =(Spot price - Breakeven point) * Lot size
= (₹2,300 - ₹2,100) * 300
= ₹60,000.
Mr. Kumar incurred a loss of ₹60,000 on this trade.
Scenario 2: At expiry, Infosys Ltd is trading at ₹2,100.
In this case, Mr. Kumar will neither make a profit nor a loss as the spot price is equal to the breakeven point of ₹2,100 mark.
Loss =(Spot price - Break even point) * Lot size
= (₹2,300 - ₹2,300)*300
= 0
Scenario 3: At expiry, Infosys Ltd is trading at ₹2,000
In this case, Mr. Kumar's view turned out to be correct and the stock did not move above the strike price. In fact, the price is ₹100 lower than the break even point. Thus, he will pocket the entire premium as his profit. As long as the spot price expires below the strike price, the writer pockets the entire premium as profit.
Profit = Total premium received = Lot size x premium received = 300 x 100 = ₹30,000.
So, Mr.Kumar's profit is ₹30,000 on this trade.
However, the maximum profit of a call option writer is the premium received by selling the option.
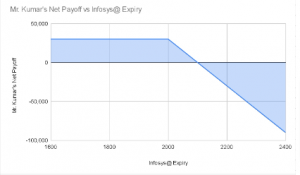
Payoff Schedule
Infosys @ Expiry | Net Payoff (₹) |
2400 | -90,000 |
2300 | -60,000 |
| 2200 | -30,000 |
2100 | 0 |
| 2000 | 30,000 |
1900 | 30,000 |
| 1800 | 30,000 |
1700 | 30,000 |
| 1600 | 30,000 |
Payoff Chart
It is essential to remember that the derivatives are a "zero-sum-game". This means that the position taken by writer and buyer are exactly opposite and therefore have an exactly opposite payoff. So, any profit received by the seller is at the loss of the buyer and vice-versa.
Covered call writing
Covered call writing is a hedging strategy. A covered call refers to selling a call option of a security that the trade already has a long position on in the cash market or in futures. This strategy is used when the holding has strong potential upside in the long term. However, it might fall in the short-term.
Summary:
- Call writing simply refers to selling a call option contract.
- The outlook of a call writer is bearish or range bound.
- The call writer earns a profit when at expiry the spot price is less than the break even point.
- Call option writer's profit potential is limited to the premium received for selling the option.
- However, his loss potential is high. The call writer incurs a loss when the spot price is more than the break even point.
- Call options are a 'zero-sum-game'. This means that the position taken by writer and buyer are exactly opposite and therefore have an exactly opposite payoff.
About Author
Upstox Desk
Upstox Desk
Team of expert writers dedicated to providing insightful and comprehensive coverage on stock markets, economic trends, commodities, business developments, and personal finance. With a passion for delivering valuable information, the team strives to keep readers informed about the latest trends and developments in the financial world.
Read more from UpstoxUpstox is a leading Indian financial services company that offers online trading and investment services in stocks, commodities, currencies, mutual funds, and more. Founded in 2009 and headquartered in Mumbai, Upstox is backed by prominent investors including Ratan Tata, Tiger Global, and Kalaari Capital. It operates under RKSV Securities and is registered with SEBI, NSE, BSE, and other regulatory bodies, ensuring secure and compliant trading experiences.