Introduction to The Option Greek - Delta
Introduction to the Option Greek – Delta
The analogy of a home loan could prove useful to understand Delta. You know how it works. If the interest rate on your home loan were to increase, your EMIs (monthly installments) would correspondingly go up. Similarly, if rates were to decrease, theoretically, your EMIs should also go down. Delta is similarly linked to the price of the underlying security. Delta tells you how much is the quantum of increase or decrease you can expect in option premium when the price of the underlying stock increases or decreases.
What is delta?
Delta is a measure of the sensitivity of an option's price to changes in the underlying asset's price. It is expressed as a number between 0 and 1 for call options and -1 and 0 for put options. The delta shows how much the option moves in value for a one-point move in the underlying asset's price. For example, if an option has a delta of 0.50, then for every one-point move in the underlying asset's price, the option's value will move by half a point.
An option contract’s delta value can be found on the option chain – there is no need to calculate it. In illustration 1 below, we have a screenshot of the Upstox option chain found on our website. We have highlighted the columns that display the delta. As you can see, there is a delta column for calls and one for puts. If you look closely, you will also see that each strike price has a different value for delta. In addition, the delta values for call options are positive and the values for put options are negative. This will always be the case.
A key point with delta, as with all of the Greeks, is that it is NOT a static value. It will change as the underlying price changes, time continues towards expiration, or volatility goes up or down.
Illustration 1
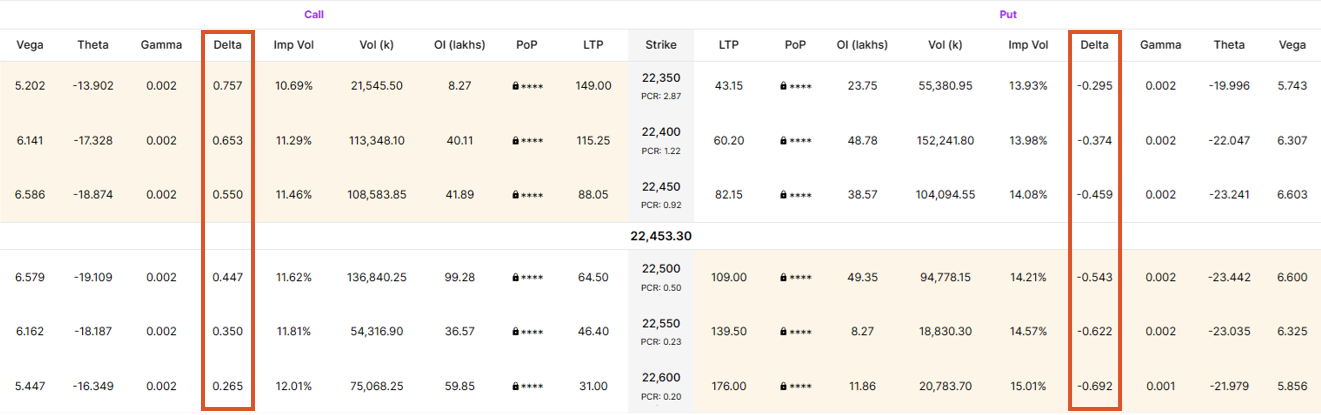 Source: Upstox
Source: UpstoxWhat is an example of using delta?
Let’s look at a hypothetical example of a stock trading for ₹100. The option chain for this stock is shown in illustration 2 below. We will examine three different call options – one for the strike price of 100, another for a strike price of 95, and the other for the strike price of 105. The 100-strike option is at-the-money, the 95-strike call option is in-the-money, and the 105-strike price is out-of-the-money.
Illustration 2
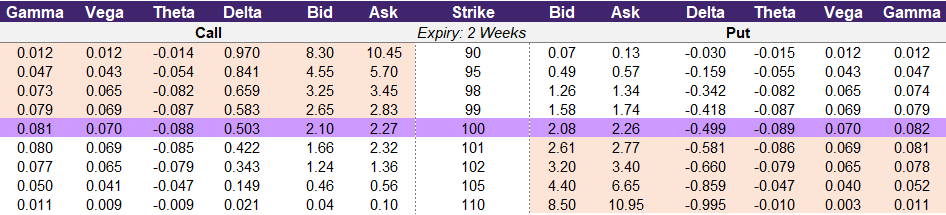 Source: Upstox
Source: UpstoxThe 100-strike price call option has an asking price of ₹2.27, which is the price you would pay to buy it, and a delta of 0.503. If the underlying asset moves up in price by ₹1 – from ₹100 to ₹101 – then this particular call option will increase in price by 0.503. The new price of the option after this underlying price move will approximately be ₹2.77 (+0.50). This is an increase of 22% for the option compared to a 1% increase for the stock. The option’s returns are so much higher due to the leverage effect of options.
For the 95-strike price call option, the price is ₹5.70 with a delta of 0.841. If this particular stock goes up in price from ₹100 to ₹101, then this option will approximately go up to ₹6.54. This is an increase in price of ₹0.84 which is a percent increase of 15%. This is a larger amount of increase than the 100-strike price (₹0.84 vs. ₹0.50) because the 95-strike price has a higher delta. However, the return is lower for the 95-strike price (15% vs. 22%) as compared to the at-the-money strike price (100-strike).
Now, let’s look at the out-of-the-money call option. The 105-strike price has a price of ₹0.56 and a delta of 0.149. The ₹1 increase in the stock will result in this option moving up in price to approximately ₹0.71 (₹0.56 + ₹0.149). This is the opposite situation of the in-the-money call option. The 95-strike price has a higher delta and the amount gained when the underlying changes in price is higher than the 105-strike price. However, the option’s return on that movement is higher for the 105-strike price (the out-of-the-money contract).
Illustration 3
| Strike | Option Price | Delta | Option Price (Stock Up ₹1) | Return (Stock Up ₹1) | Option Price (Stock Down ₹1) | Return (Stock Down ₹1) | |
|---|---|---|---|---|---|---|---|
| In-the-money | 95 | 5.70 | 0.841 | 6.54 | 14.8% | 4.86 | -14.8% |
| At-the-money | 100 | 2.27 | 0.503 | 2.77 | 22.2% | 1.77 | -22.2% |
| Out-the-money | 105 | 0.56 | 0.149 | 0.71 | 26.5% | 0.41 | -26.5% |
In the table above, we summarize the approximate price movements of these three option contracts. One thing we didn’t discuss was downward price movements. Whether the stock moves up or down, the delta will provide you with the approximate movement. In this table, you can see how the option price falls if the underlying price falls.
As a trader, knowing the delta can help you determine how much risk you are taking on when you buy or sell an option. For example, if you decide to purchase an option with a low delta value like 0.10, you will be aware that if the underlying starts to move in your favor, the rupee-value of your option will not change much. However, you may have greater risk because the percentage change of the option price could be substantial.
One last point: you should only do this calculation for a 1-unit change. As the underlying price changes, the delta value will change. In particular, if the underlying goes up in value, the delta will go up in value. Because of this, you shouldn’t try to use the delta to estimate the impact of a 2+ unit price change. In order to do this more accurately, we will need to look at another Greek: Gamma. Gamma is the change in delta based on the change in the underlying price. We will discuss gamma in another lesson.
How does delta vary between calls and puts?
In our prior example, we discussed how the price of a call option – specifically a long call option – would change based on the delta. When you look at call options in the option chain, you will see that the value of delta is positive. This means that if the underlying asset increases in value, the option will also increase in value. If the underlying falls in value, then the option will decrease in value. When you sell an option (go short an option), you are doing the opposite trade. This means that the delta is negative for a short call option. If the underlying increases in price, the option will lower in price.
Also as seen on the option chain, the value for delta is negative for put options. So, if the underlying asset increases in value, the option will decrease in value. When you short a put option, the delta will be positive. In this way, the short put option will act similar to a long call option where an increase in underlying value will result in an increase in the put option’s price. Illustration 4 below summarizes this.
Illustration 4
| Strategy | Delta | Underlying Price (Up) | Underlying Price (Down) |
|---|---|---|---|
| Long Call | Positive | Option Price ↑ | Option Price ↓ |
| Long Put | Negative | Option Price ↓ | Option Price ↑ |
| Short Call | Negative | Option Price ↓ | Option Price ↑ |
| Short Put | Positive | Option Price ↑ | Option Price ↓ |
How do you interpret delta?
As we have discussed, delta is expressed as a number between 0 and 1 or -1 and 0. Delta is unique amongst the option Greeks in that it provides you more information other than insights into how the option price will change due to changes in the underlying’s price. Delta also can provide you the hedge ratio as well as the likelihood of moneyness on expiration.
Let’s return to the same example data to walkthrough the three ways in which delta can be used. Before we get started, let’s discuss some “trader-speak”. When we talk about delta, we do it in units rather than decimals. Instead of saying “delta of point nine-one” or “delta of ninety-one percent,” we simply say “ninety-one delta” or “delta of ninety-one.” Delta is so important to option traders that they may decide on the strike-price based on the delta. For instance, traders that regularly sell put options may be comfortable with the general risk-reward associated with a particular delta regardless of the underlying asset. Traders may reference that they are selling the 30-delta strike rather than identifying the specific strike price.
Illustration 5
 Source: Upstox
Source: UpstoxSo, if the underlying which is currently trading at 100 goes by 1 (or +1.0%), then the option price will move up from 10.45 to 11.42. This gain of 0.97 in the option price represents a percent gain of 9.3%.
When options are deep in-the-money, the delta for call options will go to 1.0. The 90-strike price call option is very close to this. When a call option has a delta of 1, for each 1-unit change in the underlying, the option will also change by 1-unit. So, options with a delta of 1 move in alignment with the underlying. A bit of trivia: at some Wall Street firms, the equity trading desks are known as ‘Delta One’.
For most individuals reading this lesson, you want to be long delta because you are interested in capitalizing on market movements. On the other hand, market makers and some professional traders aren't concerned with making proprietary trades on market movements. They are only interested in facilitating market transactions. Instead of making a return if their predicted movement is correct, their return is based on earning the difference between the bid and the ask price. A market maker will want to hedge the delta so they have as minimal exposure to market movements as possible.
In this example, the 100-strike is the 50-delta line. 50-delta would tell the market maker that they need to sell the underlying security at a rate of 0.50 for every 1 call option purchased in order to have a delta of 0. Having a delta of 0 is considered to be “delta neutral”. Delta hedging is primarily for market makers. But this concept can be used by traders as they construct stock and option portfolios.
For example, in illustration 3, the 98-strike has a delta of 0.66. This means that the market is implying that there is a 66% likelihood of the underlying being at or above 98 on expiration. This likelihood isn’t a certainty and is just an implied prediction based on the market’s trading of various option contracts.
A technical point you need to know here is that there is a more accurate view of the likelihood of moneyness: this term is known as ‘Dual Delta.’ This is a more advanced topic that we won’t cover in this course. However, the difference is usually non-impactful to your decisions. In our example, the delta is 66% for the 98-strike but the dual delta could be around 62%. As a trader making a quick buy or sell decision, that difference is most likely negligible.
Let’s take this one step forward. You believe that the underlying in this example will move upwards dramatically over the next few days, so you decide to purchase the call option with a 98-strike. The price of this option is 3.45 making the break-even price 101.45 (98 + 3.45). The delta shows the likelihood of the strike price being in the money on expiry; this doesn’t mean the likelihood of the option breaking even.
In this example, you can look at the delta of the 101 and 102 strike prices. This is because the breakeven point for the 98-strike call option is between these two strikes. The delta of the 101-strike is 0.42 and the delta of the 102-strike is 0.34. The average between these two delta values is 0.38. Therefore, the likelihood that the 98-strike price call option is profitable on expiry is 38%. At least that is what the market is implying.
Is it better to trade options with higher delta or lower delta?
As a trader, you need to determine what your personal trading strategy is - how are you going to identify opportunities, how is what you are doing different than the majority of other participants, and how are you going to consistently win? Depending on your answer to this, you will also need to have a trading plan or risk management plan to minimize large losses and long stretches of losing trades. Even more specific, is your trading style "long directional" or are you focused on "premium collection" (short strategies).
The general rule of trading is that small and frequent wins are far superior to large and sporadic wins. When it comes to long strategies, options with higher delta are a better fit for frequent wins as options with higher delta will have a higher probability of expiring in-the-money. While lower delta options will have a lower cost and potential for higher ROI, your win rate will likely be far lower than with options with a higher delta. Alternatively, with short strategies, your goal is for the option to expire worthless. For this to have the best chance of happening, you will want to trade options with a low delta. Of course, with a low delta, you will receive a small premium because the option will be out-of-the-money. But similar to long strategies, selling options with a low delta will be the best approach for consistent trade wins.
What is the delta of an at-the-money (ATM) option?
The delta of an option is a measure of how much the value of the option changes when the underlying stock moves. For an at-the-money (ATM) option, the value is usually close to 0.50 for long calls (and short puts). This means that if the underlying stock moves up by ₹1, the option will increase in value by approximately ₹0.50. On the other hand, if the stock moves down by -₹1, then the option will fall by approximately -₹0.50.
For long puts (and short calls), the delta is close to -0.50 meaning that an increase in the underlying stock of ₹1 will result in a decrease in the option price of approximately -₹0.50. With a delta of -0.50,
Delta can be also be used to determine the likelihood of an option expiring in the money. If an option is at-the-money, then the delta is 0.50. Thus, the option has a 50% likelihood of being in the money on expiry. Intuitively, this makes sense as there is an equal chance that the underlying can go up or down from its current price point.
How does delta vary by moneyness for long call options?
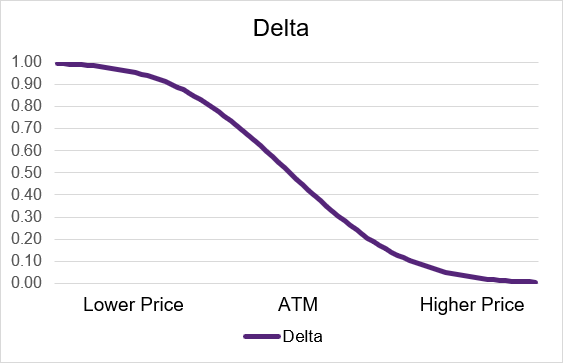
Delta is a measure of how much an option’s price will change in response to a change in the underlying asset’s price. For a long call option, the delta is positive, meaning that as the underlying asset’s price increases, so will the option’s price. The amount of the increase in the option’s price will vary depending on the moneyness of the option. For a deep in-the-money call option, the delta will be close to 1, meaning that the price move in the underlying asset will be matched by a change in the option’s price. For an at-the-money option, the delta will be close to 0.50, meaning that a ₹1 move in the underlying asset’s price will cause a smaller move of approximately ₹0.50 in the option’s price. For a deep out-of-the-money call option, the delta will be close to 0, meaning that a move in the underlying asset’s price will cause almost no change in the option’s price.
Illustration 6: Long Call Delta by moneyness
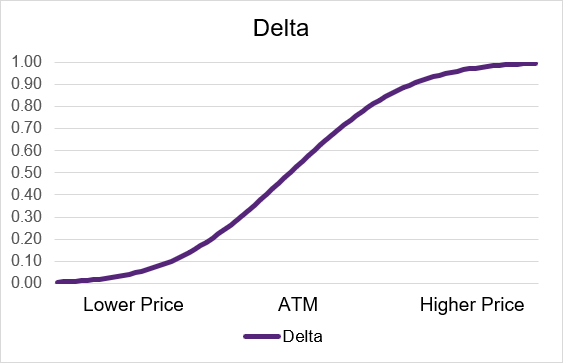 Source: Upstox
Source: UpstoxHow does delta vary by moneyness for short call options?
When a trader sells or shorts a call option, the payoff is the opposite of the long call option. Similarly, the delta values are the opposite. Instead of ranging from 0 to 1 as with a long call, the delta of a short call option ranges from -1 to 0. A short call option that is at-the-money will have a delta near -0.50. The delta of a short call option that is deep out-of-the-money will have a delta near 0. This means that price changes in the underlying asset will have minimal impact on the price of the short call option. A short call option that is deep in-the-money will have a delta near -1. With a deep in-the-money short call option, a price change of +1 in the underlying will result in a change of -1 in the option.
Illustration 7: Long Put Delta by moneyness
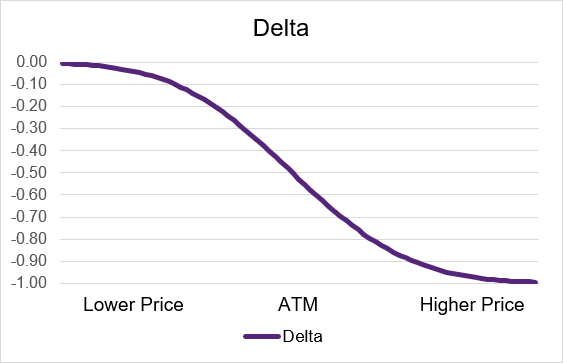 Source: Upstox
Source: UpstoxHow does delta vary by moneyness for long put options?
For long put options, as with other option types, delta will vary depending on the moneyness of the option. Moneyness refers to the relationship between the strike price of the option and the price of the underlying asset. If the underlying asset is significantly greater than the strike price, the option is said to be deep out-of-the-money and will have a negative delta approaching 0. This means that the option will have minimal price impact due to changes in the underlying’s price. If the underlying asset price is equal to the strike price, the option is said to be at-the-money and will have a delta of approximately -0.50. Finally, if the price of the underlying asset is far below the strike price, the option is said to be deep in-the-money and will have a delta close to -1.0. This means that the option will decrease in value as the underlying asset increases in value.
Illustration 8: Short Call Delta by moneyness
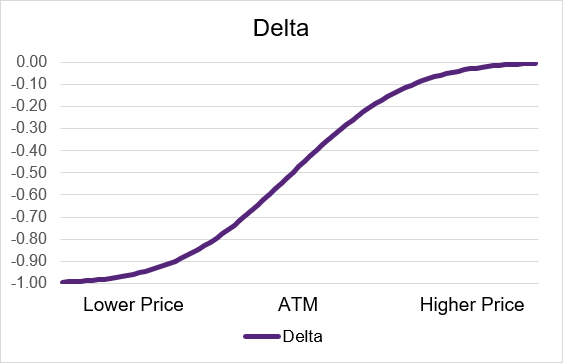 Source: Upstox
Source: UpstoxHow does delta vary by moneyness for short put options? For short put options, the value of delta ranges from +1 to 0 where delta approaches +1.0 when the underlying price is far below the strike price. If the delta is close to 1, this means that the price of the option will change in lock-step with the underlying price. For example, if the underlying goes up by ₹1, then the option will go up by approximately ₹1. Alternatively, the delta value will approach 0 when the underlying price is far above the strike price. Similar to long call options, when the option is trading at-the-money, which is when the underlying price equals the strike price, the value of delta will be approximately +0.50.
Illustration 9: Short Putl Delta by moneyness
 Source: Upstox
Source: UpstoxSummary
- Delta shows you approximate likelihood of moneyness on expiration.
- Delta for call options ranges from 0 to 1 and delta for put options ranges from -1 to 0.
- In a call option, as strike price reduces, delta gets bigger and vice-versa. The opposite is true for put options.
- The delta gets bigger as you go deeper in-the-money, and smaller as you go further out-of-the-money.
- The more in-the-money an option is, the more sensitive to the change in the underlying price.
- When Delta is 1 or close to 1, the option trades in lock-step with the underlying.
- Being ‘long delta’ means being exposed to market movements – ideal for traders.
- Hedging the delta allows minimal exposure to market movements.
- Hedge delta of a stock by buying a put option for the same stock.
Is this chapter helpful?
- Home/
- Introduction to The Option Greek - Delta